A power structure is a system of relationships among political actors with varying levels of strength. Power structures can be found in a wide variety of settings, such as the international system, national politics, local government, among competing institutions, and within organizations. Anywhere there are people struggling for power, they’re doing so within a power structure of some kind or another.
Power structure theory (PST) is a framework for modeling and understanding power structures in all of these contexts. At its core, PST boils down to three mathematical equations. There’s no need to understand them in order to grasp and appreciate the theory, because the basic ideas can be communicated visually using diagrams and animations. But for those who are curious, in this post I’m going to explain how the first of these equations — the law of motion — works. In follow up posts, I’ll cover the other two equations.
Knowing that even highly intelligent people sometimes recoil at the sight of math, I’ve tried to make this explanation as clear as I can. If you ever took algebra and are willing to let me spoon feed you the details, this can make sense. If it doesn’t, that’s on me.
Representing Power Structures
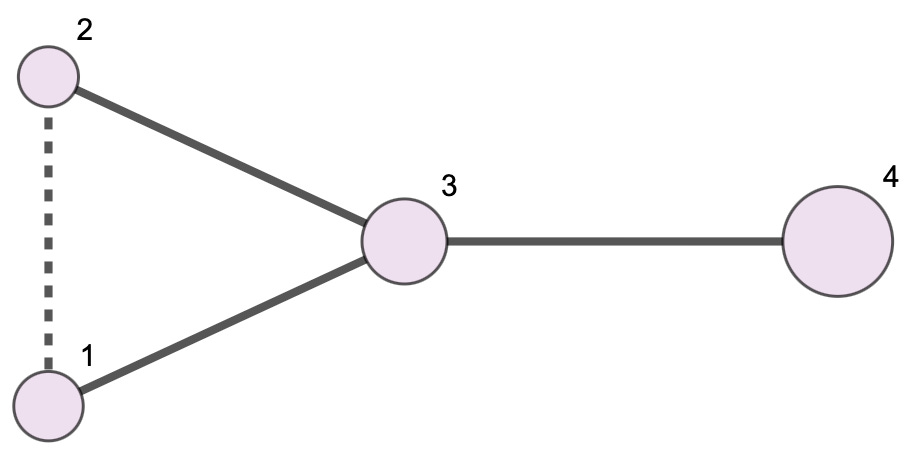
We’ll work from an example of a simple power structure, shown in the figure below. In this structure, there are four actors, each of which is numbered to make it easier for us to refer to them. This is called the index number of each actor. These four actors have relationships with each other. Solid lines denote cooperation, which causes actors to get stronger. The dashed line indicates conflict, which causes them to get weaker. Some pairs of actors, such as 2 and 4, have no relationship with each other at all, and therefore no connecting line. Actors with larger circles are stronger; those with smaller circles are weaker.
Now let’s talk about the numeric data representing this structure. The sizes of the actors — that is, how powerful each one is relative to the others — are stored in a list called a size vector, denoted by the variable s. The size vector for the power structure above is:
This means that the actor with index number 1 has a size of 0.4, actor 2 has a size of 0.3, etc. The strongest actor, number 4, has a size of 1. The sizes of the nodes in the diagram are proportional to the corresponding numbers in the size vector.
Knowledge check: What is the size of the actor with index number 3?1
The relationships among the actors are represented numerically in a tactic matrix, denoted by T. A matrix is just a list of lists, or a rectangular way of storing data. The tactic matrix for our power structure is:
The tactic matrix describes how the actors in the power structure are using the power that they have. Each column represents the “foreign policy” of one of the actors — that is, how it behaves towards others.
For example, in the first column on the left — corresponding to index number 1 — the 0.98 means that 98% of actor 1’s power is being kept to itself. The entire diagonal from the top left to the bottom right of the matrix contains the self-allocations of the four actors — that is, how much of their power they are keeping rather than transmitting to others. This diagonal shows that most power is retained rather than transferred to other actors; this is typical in a tactic matrix.
The second entry in that first column, which has the value of -0.01, means that 1% of actor 1’s power is being directed destructively at actor 2 (because this is the second entry from the top in that column). Negative values in the tactic matrix represent destructive power. Positive values mean constructive transfers of power. Zero values mean no transfer at all. In the next section, I’ll explain the significance of these uses of power.
Notice that if you pretend that all of the numbers in the tactic matrix are positive, each column would add up to 1. This is because each column has to account for 100% of that actor’s power.
Knowledge check: How much of actor 3’s power is being directed at actor 4?2 Is this transfer destructive, constructive, or neutral?3 Which actor is keeping the largest percentage of power to itself?4
The key takeaway thus far is that a power structure is primarily composed of two data objects: a size vector that represents how powerful each actor is, and a tactic matrix that describes their relationships.
The Effects of Interactions
What happens when the actors in a power structure interact? Each actor can cause every other actor to get larger or smaller, in other words more powerful or less powerful. They do this through the constructive or destructive transfers of power that are listed in the tactic matrix.
Destructive transfers
To explain how the law of motion works, let’s start with destructive transfers of power. In our power structure example, actor 1 is attacking actor 2. This means that actor 1 is directing 1% of its power negatively at actor 2. So actor 1’s power goes down by 1%. When actor 2 receives that transfer, it’s power level goes down by the amount of that transfer, multiplied by a parameter called mu, or μ (sorry, but the parameters are represented by Greek letters). This destructive multiplier means that transfers of negative power cause damage to the recipient.
Think of this in terms of money. It would be like actor 1 is spending $1 to hurt actor 2, but the damage comes to more than $1. For example, maybe actor 1 bought an X-Acto blade and slashed actor 2’s car tire.
Let’s walk through the arithmetic of what actor 1 is doing to actor 2 step by step. Actor 1 has a size of 0.4, and 1% of that is 0.004. When actor 1 takes this action, it’s own size decreases by 0.004 to become 0.396. This represents the energy it is expending. Let’s assume that the destructive multiplier is 10. Actor 2’s size, which started as 0.3, decreases by 0.004 times 10, or 0.04. So actor 2 ends up with a size of 0.26 by virtue of being attacked.
In our power structure, actors 1 and 2 are attacking each other, so this process is actually bidirectional. Each is reduced by the expenditure of its own power, and each is reduced further from the enemy’s attack.
Constructive transfers
Ok, now what happens when actors are nice to each other? When positive or constructive power is transferred, it’s a similar process. An actor expends positive power, so their own power goes down and the recipient’s power increases. But it’s not like giving someone a $1 bill. It’s more like giving them a $1 bill but when they take it from your hand, it’s suddenly worth more than $1. How much more? That depends on another Greek parameter call beta, or β, which is the constructive multiplier. The constructive multiplier defines how much of an increase occurs. When two actors mutually exchange constructive power, they both get more powerful. In other words, there are gains from cooperation, and β says how much those gains are.
Let’s walk through an example. In our power structure, actor 3 is making a constructive transfer of 1% to actor 4. Actor 3’s size is 0.6, so this transfer causes its size to be reduced by 0.006, resulting in a new size of 0.594. When actor 4 receives this gift, its value has magically increased by the constructive multiplier. Let’s assume for this example that β=2, meaning that actor 4 receives 0.006 times 2, or 0.012. Actor 4’s size therefore goes from 1.0 to 1.012.
Intrinsic growth
Power that is not allocated to others can grow, shrink, or stay the same. It all depends on yet another Greek parameter called lambda, or λ. If this intrinsic growth rate is greater than 1, then the power that an actor holds on to grows, as if they put their money in a savings account with interest. If lambda is less than 1, then their retained power shrinks. And if λ=1, it stays the same. The important thing here is that the intrinsic growth rate is always less than the constructive multiplier (that is, λ < β). The reason is that there needs to be an incentive for actors to cooperate, and if beta were ever less than lambda, it would make more sense for the actors to keep their power to themselves than to interact constructively with each other. To keep things simple in our example, let’s just assume that λ=1.
The Law of Motion
Now it’s time to combine all of these transfers and multipliers and find out what our updated size vector is. The law of motion describes this process of change. It combines the size vector and the tactic matrix together in a mathy way that I’m about to explain, and it gives us a new size vector representing the updated power levels of the actors.
Let’s start with the equation below. On the left side of this equation is the size vector s at the next time step, denoted as t+1. This means that this equation is going to tell us what will happen in the future. On the right side, we have an expression giving us the rule for updating the size vector.
Let’s start from inside the parentheses. T' (pronounced “T prime”) is a modified version of our tactic matrix from above. It represents T with each value multiplied by the appropriate Greek constant. Every value in the matrix diagonal is multiplied by the intrinsic growth rate, which we’re assuming is 1. The positive values are multiplied by μ, which is 2. And the negative values are multiplied by β, which is 10.
Here’s how we get T'. First, we need to break up T into three component matrices, one representing the matrix diagonal; one with its (non-diagonal) positive values, and one with its (non-diagonal) negative values:
For our example power structure, these components would be
If you were to add these three components together by “superimposing” them on top of each other, you’d get our original tactic matrix. We’ve just broken it into three separate pieces so we can apply the appropriate multiplier to each one.
To get T', we multiply each of the component matrices by the appropriate parameter. The formula for this is:
Plugging in the values from our example and applying the multipliers, we get:
Which adds up to:
Now look back at that first equation above. Still within the parentheses, it says that we’re going to multiply T' and s at time t (in other words, the initial value of s). When you multiply a matrix by a vector, you get a new vector. I won’t go into the details, but here’s a Khan Academy explanation of how this operation works. In our example, the result would be:
The size vectors above are printed vertically instead of horizontally, which is a mathematical convention. Notice that in the resulting size vector on the right, actors 1 and 2 (in the top two slots in the list) got smaller, while actors 3 and 4 got larger. This is the result of those transfers of destructive and constructive power, respectively.
There’s just one more part of the first equation above that I didn’t explain, and it’s the Ramp function. All this does is make sure that no values in the size vector ever go below zero. In other words, if an actor loses all of their power and “dies”, they stay at zero instead of having a negative size.
Summarizing, to understand how actor sizes in a power structure change over time, we: (1) apply the multipliers to the tactic matrix T; (2) multiply the resulting T' with the initial size vector s; and (3) make sure that no values go below 0. Simple!
Wrap Up
Putting all of the pieces together, I prefer to express the law of motion like this, with the three parameters explicitly included:
What’s the point of all this? The point is that power structures are dynamic. When we look at one and perceive how strong the various actors are and understand their relationships, there’s an implication about how that system is going to change over time. Some of the actors will get stronger, and others will get weaker. The law of motion tells us what specific changes we can expect as a result.
The processes described by the law of motion are more comprehensible once you see them visually. Below is an animation showing how our power structure will evolve over time as the actors’ relationships cause each other’s power levels to change.5 All we’re doing is applying the law of motion repeatedly over multiple time steps:
The real significance of power structures and the law of motion is that this abstraction pops up in a wide variety of political situations and, as a result, it helps us understand something fundamental about political processes.
Knowledge check: Which actor would you least want to be in the animation above?6
Advanced knowledge check: If you look carefully at the animation, actor 1 first shrinks but then later starts to expand. Why?7
0.6
1%
Constructive
Actor 4, with 99%
Full disclosure: the tactic matrix used in this animation is a modified version of the one described in the text. This was necessary in order to generate a smooth, 4 second animation. Had I used the animation version of T in the text, there would have been too many decimal places for readers to contend with.
Actor 2, because it’s power dwindles as time goes on. Unless you’re into that.
I’m not telling. Struggle with it.